修正 C++ 的程式碼在使用一定量動態記憶體後會產生 RF 的問題 @ 2019/12/6 4:45pm
Submit Ranklist
Problem : 122 - [Interactive]外星人
Problem Statistics
Solved Member: 12 Submission: 174 User Tried: 13Statement:
請在程式碼加入#include "interactive/122.h"回答問題。
馬可(Mirko)是一個麥田神祕圓圈迷,麥田神祕圓圈為疑似由外星人形成的穀物株幹被壓平的幾何造形。在夏天的晚上馬可決定在祖母的麥田中做他的麥田造型。馬可是克羅埃西亞愛國人士,因此決定使用克國軍服的西洋棋盤造型,此造型為一個5x5西洋棋盤包含13個紅格子和12個白格子。

*克國軍服的西洋棋盤造型
馬可祖母的麥田為由NxN細格所構成的正方形。設麥田左下角細格的座標為(1,1), 而麥田右上角細格的座標為(N,N)。
馬可決定只將西洋棋盤內的紅格子內的麥株壓平,而不動其餘區域。他取一個奇數M≧3做為紅格子的邊長,並以MxM的細格來構成一個紅格子,以形成如下圖所示的克國軍服的西洋棋盤造型:
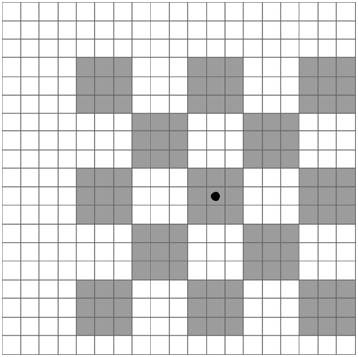
*馬可完成的麥田西洋棋盤造型範例,其中 N=19 且 M=3。麥株被壓平的細格以灰色顯示西洋棋盤造型的中心點在 (12, 9) 上,以黑色圓點表示。
馬可在祖母的麥田上完成西洋棋盤造型,去就寢之後。麥田的特殊造型引起真正外星人的興趣,外星人用一個簡單裝置在麥田上空檢查馬可的造型。此裝置只能判斷某個細格內的麥株是直立還是被壓平。外星人已經發現一個麥株被壓平的細格。現在需要找到馬可的西洋棋盤造型傑作的中心點,讓他們可以體會其美感。外星人並不知道馬可的西洋棋盤造型內每一個紅格子的大小M。
請寫一個程式給定麥田的大小N (15 ≤ N ≤ 2 000 000 000),和一個麥株被壓平細格的座標(X0, Y0),此程式並能和外星人的裝置互動。請找出馬可所做西洋棋盤造型的中心點的座標。
限制:此裝置最多只能使用300次
馬可(Mirko)是一個麥田神祕圓圈迷,麥田神祕圓圈為疑似由外星人形成的穀物株幹被壓平的幾何造形。在夏天的晚上馬可決定在祖母的麥田中做他的麥田造型。馬可是克羅埃西亞愛國人士,因此決定使用克國軍服的西洋棋盤造型,此造型為一個5x5西洋棋盤包含13個紅格子和12個白格子。

*克國軍服的西洋棋盤造型
馬可祖母的麥田為由NxN細格所構成的正方形。設麥田左下角細格的座標為(1,1), 而麥田右上角細格的座標為(N,N)。
馬可決定只將西洋棋盤內的紅格子內的麥株壓平,而不動其餘區域。他取一個奇數M≧3做為紅格子的邊長,並以MxM的細格來構成一個紅格子,以形成如下圖所示的克國軍服的西洋棋盤造型:

*馬可完成的麥田西洋棋盤造型範例,其中 N=19 且 M=3。麥株被壓平的細格以灰色顯示西洋棋盤造型的中心點在 (12, 9) 上,以黑色圓點表示。
馬可在祖母的麥田上完成西洋棋盤造型,去就寢之後。麥田的特殊造型引起真正外星人的興趣,外星人用一個簡單裝置在麥田上空檢查馬可的造型。此裝置只能判斷某個細格內的麥株是直立還是被壓平。外星人已經發現一個麥株被壓平的細格。現在需要找到馬可的西洋棋盤造型傑作的中心點,讓他們可以體會其美感。外星人並不知道馬可的西洋棋盤造型內每一個紅格子的大小M。
請寫一個程式給定麥田的大小N (15 ≤ N ≤ 2 000 000 000),和一個麥株被壓平細格的座標(X0, Y0),此程式並能和外星人的裝置互動。請找出馬可所做西洋棋盤造型的中心點的座標。
限制:此裝置最多只能使用300次
Task:
此題提供三個函式:
void init(int &N, int &X0, int &Y0):指定 N,X0,Y0 的值。
bool examine(int X, int Y):檢查麥田中(X,Y)是否是壓平的,若是回傳true,否則回傳false。
void solution(int Xc, int Yc):告訴程式你已經找到中心為(Xc, Yc),並自動結束程式。
• 你的程式一開始應由 init 函式讀入三個整數 N,X0 和 Y0,各數之間空一格。整數 N 為麥田的邊長,而(X0,Y0)為已知是麥株被壓平細格的座標值。
• 為了以外星人裝置來檢查麥田的一個(X,Y)細格,你必須執行 examine(X,Y)。若座標(X,Y)不在麥田的範圍內(亦即不滿足1≦X≦N且1≦Y≦N的條件),或你的程式使用外星人裝置已經超過300次,你的程式在跑測試資料時,將會得到0分。
• 外星人裝置檢查麥田的(X,Y)細格時,若麥株是被壓平的,即回傳true;若麥株直立則回覆false。
• 若你的程式已經發現西洋棋盤造型的中心點座標,需要執行函式 solution(Xc,Yc),代表中心點的座標值為(Xc,Yc)。此時你的程式在輸出此行結果後應能自動結束。
void init(int &N, int &X0, int &Y0):指定 N,X0,Y0 的值。
bool examine(int X, int Y):檢查麥田中(X,Y)是否是壓平的,若是回傳true,否則回傳false。
void solution(int Xc, int Yc):告訴程式你已經找到中心為(Xc, Yc),並自動結束程式。
• 你的程式一開始應由 init 函式讀入三個整數 N,X0 和 Y0,各數之間空一格。整數 N 為麥田的邊長,而(X0,Y0)為已知是麥株被壓平細格的座標值。
• 為了以外星人裝置來檢查麥田的一個(X,Y)細格,你必須執行 examine(X,Y)。若座標(X,Y)不在麥田的範圍內(亦即不滿足1≦X≦N且1≦Y≦N的條件),或你的程式使用外星人裝置已經超過300次,你的程式在跑測試資料時,將會得到0分。
• 外星人裝置檢查麥田的(X,Y)細格時,若麥株是被壓平的,即回傳true;若麥株直立則回覆false。
• 若你的程式已經發現西洋棋盤造型的中心點座標,需要執行函式 solution(Xc,Yc),代表中心點的座標值為(Xc,Yc)。此時你的程式在輸出此行結果後應能自動結束。
Input:Output:
無輸入
無輸出
HINT:
範例(圖形與第二張圖相符):
佔總分40分的測試資料中,每個馬可的麥田造型的 M 值至少100以上。
| 詢問 | 結果 |
|---|---|
| init(N, X0, Y0); | N=19; X0=7; Y0=4 |
| examine(11,2); | true |
| examine(2,5); | false |
| examine(9,14); | false |
| examine(18,3); | true |
| solution(12,9); | 答對了! |
佔總分40分的測試資料中,每個馬可的麥田造型的 M 值至少100以上。
Source:
IOI 2007Problem Setter
NekosyndromeTestdata:
| Test | Time | Memory | Score |
|---|---|---|---|
| 0 | 1000ms | 65536kb | |
| 1-1 | 1000ms | 65536kb | 10 |
| 1-2 | 1000ms | 65536kb | |
| 2-1 | 1000ms | 65536kb | 10 |
| 2-2 | 1000ms | 65536kb | |
| 3-1 | 1000ms | 65536kb | 10 |
| 3-2 | 1000ms | 65536kb | |
| 4-1 | 1000ms | 65536kb | 10 |
| 4-2 | 1000ms | 65536kb | |
| 5-1 | 1000ms | 65536kb | 10 |
| 5-2 | 1000ms | 65536kb | |
| 6-1 | 1000ms | 65536kb | 10 |
| 6-2 | 1000ms | 65536kb | |
| 7-1 | 1000ms | 65536kb | 10 |
| 7-2 | 1000ms | 65536kb | |
| 7-3 | 1000ms | 65536kb | |
| 8-1 | 1000ms | 65536kb | 10 |
| 8-2 | 1000ms | 65536kb | |
| 8-3 | 1000ms | 65536kb | |
| 9-1 | 1000ms | 65536kb | 10 |
| 9-2 | 1000ms | 65536kb | |
| 9-3 | 1000ms | 65536kb | |
| 10-1 | 1000ms | 65536kb | 10 |
| 10-2 | 1000ms | 65536kb | |
| 10-3 | 1000ms | 65536kb |
NeoHOJ — The new era of HOJ
頁面讀取時間: 0.0132 秒,使用記憶體: 0.46MB 。
GitHub