修正 C++ 的程式碼在使用一定量動態記憶體後會產生 RF 的問題 @ 2019/12/6 4:45pm
Submit Ranklist
Problem : 243 - Kunai
Problem Statistics
Solved Member: 2 Submission: 8 User Tried: 2Statement:
苦無(Kunai) 是一個刀子形狀的尖銳武器,忍者會對他們的敵人投擲苦無。
現在有 N 名忍者在 H 列 W 行的方陣中,每名忍者在格子的正中央,並且一個格子不會有兩名以上的忍者。每名忍者都有一把苦無,並且面向上、下、左、右四個方向中的其中一個方向。在時間點0 時,每名忍者朝他們面向的方向投擲出苦無。
每把苦無以速度1 直線前進,如果有不止一把苦無在同一時間飛到同一地點,它們會破撞並且消失。我們可以忽略苦無的大小。另外,由於忍者可以快速移動,所以他們不會被苦無擊中。每把苦無會以等速直線飛行,除非和另外的苦無碰撞。
在下圖中,箭頭代表苦無,箭頭方向代表苦無飛行的方向,在這些圖中,所有粗體的箭頭都會發生碰撞。
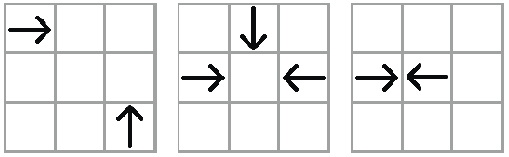
而在下列圖中,粗箭頭並不會和另一個粗箭頭相撞。第二和第三張圖中,細箭頭會和一個粗箭頭相撞。因為相撞的箭頭會消失,因此這兩張圖中各有一個粗箭頭不會發生碰撞而會持續飛行。
![]()
現在有 N 名忍者在 H 列 W 行的方陣中,每名忍者在格子的正中央,並且一個格子不會有兩名以上的忍者。每名忍者都有一把苦無,並且面向上、下、左、右四個方向中的其中一個方向。在時間點0 時,每名忍者朝他們面向的方向投擲出苦無。
每把苦無以速度1 直線前進,如果有不止一把苦無在同一時間飛到同一地點,它們會破撞並且消失。我們可以忽略苦無的大小。另外,由於忍者可以快速移動,所以他們不會被苦無擊中。每把苦無會以等速直線飛行,除非和另外的苦無碰撞。
在下圖中,箭頭代表苦無,箭頭方向代表苦無飛行的方向,在這些圖中,所有粗體的箭頭都會發生碰撞。

而在下列圖中,粗箭頭並不會和另一個粗箭頭相撞。第二和第三張圖中,細箭頭會和一個粗箭頭相撞。因為相撞的箭頭會消失,因此這兩張圖中各有一個粗箭頭不會發生碰撞而會持續飛行。
Task:
請計算足夠長的時間後,在 W×H 方格中有多少方格會有苦無飛過。
Input:Output:
第一行輸入兩個用空白隔開的整數W 和H,代表方陣的大小。
第二行輸入一個整數N,代表忍者的數量。
接下來的N 行中的第i 行(1 ≤ i ≤ N) 有三個用空白隔開的整數Xi、Yi、Di,代表忍者 i 位在第 Xi 行(從左而右)和第 Yi 列(從上而下)的格子;Di 代表忍者i 面對的方向。
Di = 0 表示忍者i 面對右方。
Di = 1 表示忍者i 面對上方。
Di = 2 表示忍者i 面對左方。
Di = 3 表示忍者i 面對下方。
可以保證:
忍者數量(N), 1 ≤ N ≤ 100 000
方陣大小(W, H), 1 ≤ W ≤ 1 000 000 000, 1 ≤ H ≤ 1 000 000 000
忍者座標(Xi, Yi), 1 ≤ Xi ≤ W, 1 ≤ Yi ≤ H
N ≤ 1 000,W ≤ 1 000,H ≤ 1 000 的測試資料佔分10%。
N ≤ 1 000 的測試資料佔分40%。
第二行輸入一個整數N,代表忍者的數量。
接下來的N 行中的第i 行(1 ≤ i ≤ N) 有三個用空白隔開的整數Xi、Yi、Di,代表忍者 i 位在第 Xi 行(從左而右)和第 Yi 列(從上而下)的格子;Di 代表忍者i 面對的方向。
Di = 0 表示忍者i 面對右方。
Di = 1 表示忍者i 面對上方。
Di = 2 表示忍者i 面對左方。
Di = 3 表示忍者i 面對下方。
可以保證:
忍者數量(N), 1 ≤ N ≤ 100 000
方陣大小(W, H), 1 ≤ W ≤ 1 000 000 000, 1 ≤ H ≤ 1 000 000 000
忍者座標(Xi, Yi), 1 ≤ Xi ≤ W, 1 ≤ Yi ≤ H
N ≤ 1 000,W ≤ 1 000,H ≤ 1 000 的測試資料佔分10%。
N ≤ 1 000 的測試資料佔分40%。
輸出在 W×H 方陣中經過足夠的時間後,苦無飛行過的格子數量。
Sample Input:Sample Output:
Sample Input 1:
5 4
5
3 3 2
3 2 0
4 2 2
5 4 1
1 1 3
Sample Input 2:
7 6
12
3 2 3
6 3 2
7 1 3
1 5 0
3 6 1
6 6 1
4 5 2
1 3 0
6 5 2
5 1 2
6 4 3
4 1 3
5 4
5
3 3 2
3 2 0
4 2 2
5 4 1
1 1 3
Sample Input 2:
7 6
12
3 2 3
6 3 2
7 1 3
1 5 0
3 6 1
6 6 1
4 5 2
1 3 0
6 5 2
5 1 2
6 4 3
4 1 3
Sample Output 1:
11
Sample Output 2:
29
11
Sample Output 2:
29
HINT:
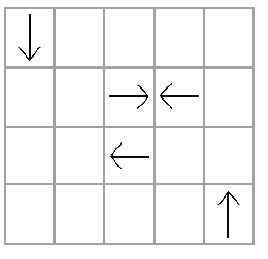
關於Sample Input 1:
時間點0 的狀態如下。
忍者i 投出的苦無稱為苦無i。在時間點0.5 時,苦無2 和3 會碰撞而消滅。下圖描述時間點1 時的狀態。灰色格子代表苦無飛行過的格子。
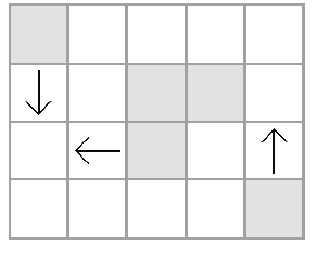
在時間點2,苦無1 和5 會碰撞而消滅。時間點2 時狀態如下圖所示。
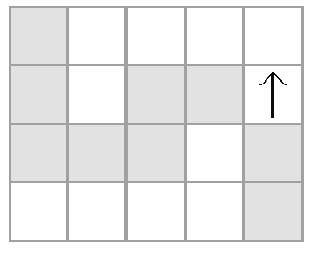
時間點2 之後不會有任何的苦無碰撞,經過一段時間後狀態如下圖所示。
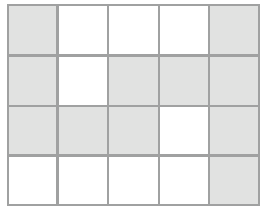
最後,所有苦無飛行經過的格子數為11,因此輸出11。
時間點0 的狀態如下。

忍者i 投出的苦無稱為苦無i。在時間點0.5 時,苦無2 和3 會碰撞而消滅。下圖描述時間點1 時的狀態。灰色格子代表苦無飛行過的格子。

在時間點2,苦無1 和5 會碰撞而消滅。時間點2 時狀態如下圖所示。

時間點2 之後不會有任何的苦無碰撞,經過一段時間後狀態如下圖所示。

最後,所有苦無飛行經過的格子數為11,因此輸出11。
Source:
APIO 2012Problem Setter
hanhan0912Testdata:
| Test | Time | Memory | Score |
|---|---|---|---|
| 0-1 | 6000ms | 262144kb | |
| 0-2 | 6000ms | 262144kb | |
| 1-1 | 6000ms | 262144kb | 10 |
| 1-2 | 6000ms | 262144kb | |
| 1-3 | 6000ms | 262144kb | |
| 1-4 | 6000ms | 262144kb | |
| 1-5 | 6000ms | 262144kb | |
| 1-6 | 6000ms | 262144kb | |
| 2-1 | 6000ms | 262144kb | 10 |
| 2-2 | 6000ms | 262144kb | |
| 2-3 | 6000ms | 262144kb | |
| 2-4 | 6000ms | 262144kb | |
| 2-5 | 6000ms | 262144kb | |
| 3-1 | 6000ms | 262144kb | 10 |
| 3-2 | 6000ms | 262144kb | |
| 3-3 | 6000ms | 262144kb | |
| 3-4 | 6000ms | 262144kb | |
| 3-5 | 6000ms | 262144kb | |
| 4-1 | 6000ms | 262144kb | 10 |
| 4-2 | 6000ms | 262144kb | |
| 4-3 | 6000ms | 262144kb | |
| 4-4 | 6000ms | 262144kb | |
| 4-5 | 6000ms | 262144kb | |
| 5-1 | 6000ms | 262144kb | 10 |
| 5-2 | 6000ms | 262144kb | |
| 5-3 | 6000ms | 262144kb | |
| 5-4 | 6000ms | 262144kb | |
| 5-5 | 6000ms | 262144kb | |
| 5-6 | 6000ms | 262144kb | |
| 6-1 | 6000ms | 262144kb | 10 |
| 6-2 | 6000ms | 262144kb | |
| 6-3 | 6000ms | 262144kb | |
| 6-4 | 6000ms | 262144kb | |
| 6-5 | 6000ms | 262144kb | |
| 6-6 | 6000ms | 262144kb | |
| 7-1 | 6000ms | 262144kb | 10 |
| 7-2 | 6000ms | 262144kb | |
| 7-3 | 6000ms | 262144kb | |
| 7-4 | 6000ms | 262144kb | |
| 7-5 | 6000ms | 262144kb | |
| 7-6 | 6000ms | 262144kb | |
| 8-1 | 6000ms | 262144kb | 10 |
| 8-2 | 6000ms | 262144kb | |
| 8-3 | 6000ms | 262144kb | |
| 8-4 | 6000ms | 262144kb | |
| 8-5 | 6000ms | 262144kb | |
| 8-6 | 6000ms | 262144kb | |
| 9-1 | 6000ms | 262144kb | 10 |
| 9-2 | 6000ms | 262144kb | |
| 9-3 | 6000ms | 262144kb | |
| 9-4 | 6000ms | 262144kb | |
| 9-5 | 6000ms | 262144kb | |
| 9-6 | 6000ms | 262144kb | |
| 10-1 | 6000ms | 262144kb | 10 |
| 10-2 | 6000ms | 262144kb | |
| 10-3 | 6000ms | 262144kb | |
| 10-4 | 6000ms | 262144kb | |
| 10-5 | 6000ms | 262144kb | |
| 10-6 | 6000ms | 262144kb |
NeoHOJ — The new era of HOJ
頁面讀取時間: 0.0177 秒,使用記憶體: 0.48MB 。
GitHub