修正 C++ 的程式碼在使用一定量動態記憶體後會產生 RF 的問題 @ 2019/12/6 4:45pm
Submit Ranklist
Problem : 262 - Crocodile
Problem Statistics
Solved Member: 9 Submission: 30 User Tried: 9Statement:
當考古學家Benjamas 調查一個神祕的鱷魚地下城市後,她想立刻逃離這個城市。這個城市有N 個密室,同時有M 個雙向的通道,沒有兩個通道會連接同一對密室,且通過每個通道的時間不盡相同。這N 個密室中,只有K 個密室有出口可以逃出去。Benjamas 從密室0 開始逃跑,並想盡快到達一個有出口的密室。
這個城市的守護者想要阻止Benjamas 逃跑,他可以控制密門來擋住任一通道;也就是說,當新密門擋住某個通道時,前一個擋住通道的密門會被打開。
Benjamas 的情況如下:每次當她想從一個密室離開時,守護者可能會擋住連接這個密室的其中一個通道。Benjamas 就會從剩下暢通的通道中選擇其一進到另一個密室。當Benjamas進入某個通道後,守護者就不能阻擋這個通道,直到她到達另一個密室為止。當Benjamas到達另一個密室後,守護者可以再次選擇擋住連接此密室的其中一個通道(包含Benjamas剛經過的通道)。
Benjamas 想要事先找到一個簡單的逃跑計畫;更精確地說,她想要一些指令集告訴她在某個密室時該怎麼做。假設A 是一個有出口的密室,顯然的她不需要任何指令就可以逃離。
否則當她在密室A 時,相關指令必須是以下形式之一:
•「如果到了密室 A,就選擇通往密室B 的通道。但是,如果這個通道被阻擋住了,就選擇通往密室C 的通道。」
•「不用考慮密室 A,因為在這份逃跑計畫中根本不可能到達密室A。」
請注意,在某些情況下(例如讓Benjamas 繞圈圈),守護者可能讓Benjamas 無法逃出去。
如果有個逃跑計畫,不管守護者會怎麼行動,都能保證Benjamas 可以在有限的時間內到達有出口的密室,這就是一個好的逃跑計畫。對於一個好的逃跑計畫,若可以保證在 T 時間後,Benjamas 一定可以到達有出口的密室,且 T 為最小值,則我們稱這個好的逃跑計畫需要 T 時間。
這個城市的守護者想要阻止Benjamas 逃跑,他可以控制密門來擋住任一通道;也就是說,當新密門擋住某個通道時,前一個擋住通道的密門會被打開。
Benjamas 的情況如下:每次當她想從一個密室離開時,守護者可能會擋住連接這個密室的其中一個通道。Benjamas 就會從剩下暢通的通道中選擇其一進到另一個密室。當Benjamas進入某個通道後,守護者就不能阻擋這個通道,直到她到達另一個密室為止。當Benjamas到達另一個密室後,守護者可以再次選擇擋住連接此密室的其中一個通道(包含Benjamas剛經過的通道)。
Benjamas 想要事先找到一個簡單的逃跑計畫;更精確地說,她想要一些指令集告訴她在某個密室時該怎麼做。假設A 是一個有出口的密室,顯然的她不需要任何指令就可以逃離。
否則當她在密室A 時,相關指令必須是以下形式之一:
•「如果到了密室 A,就選擇通往密室B 的通道。但是,如果這個通道被阻擋住了,就選擇通往密室C 的通道。」
•「不用考慮密室 A,因為在這份逃跑計畫中根本不可能到達密室A。」
請注意,在某些情況下(例如讓Benjamas 繞圈圈),守護者可能讓Benjamas 無法逃出去。
如果有個逃跑計畫,不管守護者會怎麼行動,都能保證Benjamas 可以在有限的時間內到達有出口的密室,這就是一個好的逃跑計畫。對於一個好的逃跑計畫,若可以保證在 T 時間後,Benjamas 一定可以到達有出口的密室,且 T 為最小值,則我們稱這個好的逃跑計畫需要 T 時間。
Input:Output:
第一行有N、M 和K,分別表示密室, 通道與出口的個數。
接下來有 M 行,每行有三個整數Ai Bi Ci,中間用空白隔開,表示密室Ai 與密室Bi 由一條要花 Ci 時間通過的通到所連接。
第 M+2 行有 K 個空白隔開的整數,表示出口位置。
Subtask 1 (46 points)
•3 ≤ N ≤ 1 000.
•這個地下城市是樹狀結構;也就是說, M = N-1 而且對於任兩個密室i 和j,都有一連串相連的通道能夠從密室i 連通到密室j。
•每一個可逃跑密室都只連接到另一個密室。
•其他密室都連接到三個以上的密室。
Subtask 2 (43 分)
•3 ≤ N ≤ 1 000.
•2 ≤ M ≤ 100 000.
Subtask 3 (11 分)
•3 ≤ N ≤ 100 000.
•2 ≤ M ≤ 1 000 000.
接下來有 M 行,每行有三個整數Ai Bi Ci,中間用空白隔開,表示密室Ai 與密室Bi 由一條要花 Ci 時間通過的通到所連接。
第 M+2 行有 K 個空白隔開的整數,表示出口位置。
Subtask 1 (46 points)
•3 ≤ N ≤ 1 000.
•這個地下城市是樹狀結構;也就是說, M = N-1 而且對於任兩個密室i 和j,都有一連串相連的通道能夠從密室i 連通到密室j。
•每一個可逃跑密室都只連接到另一個密室。
•其他密室都連接到三個以上的密室。
Subtask 2 (43 分)
•3 ≤ N ≤ 1 000.
•2 ≤ M ≤ 100 000.
Subtask 3 (11 分)
•3 ≤ N ≤ 100 000.
•2 ≤ M ≤ 1 000 000.
你的程式必須輸出所有好的逃跑計畫中的最小所需時間 T 。你可以假設每個沒有出口的密室都至少會有兩個連接通道。
你也可以假設每一個測試資料都有一個好的逃跑計畫,且時間 T ≤ 1 000 000 000。
你也可以假設每一個測試資料都有一個好的逃跑計畫,且時間 T ≤ 1 000 000 000。
Sample Input:Sample Output:
Sample #1:
5 4 3
0 1 2
0 2 3
3 2 1
2 4 4
1 3 4
Sample #2:
5 7 2
0 2 4
0 3 3
3 2 2
2 1 10
0 1 100
0 4 7
3 4 9
1 3
5 4 3
0 1 2
0 2 3
3 2 1
2 4 4
1 3 4
Sample #2:
5 7 2
0 2 4
0 3 3
3 2 2
2 1 10
0 1 100
0 4 7
3 4 9
1 3
Sample #1:
7
Sample #2:
14
7
Sample #2:
14
HINT:
Sample #1:
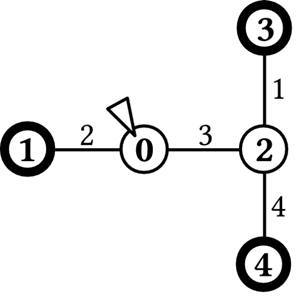
密室用圓圈表示,連接密室的通道用直線表示。有出口的密室用粗圓圈表示。Benjamas 一開始在密室0(有三角形標示處)。一個最佳的逃跑計畫如下:
•如果到了密室 0,就選擇通往密室1 的通道;如果這個通道被擋住了,就選擇通往密室2 的通道。
•如果到了密室 2,就選擇通往密室3 的通道;如果這個通道被擋住了,就選擇通往密室4 的通道。
在最壞的情況下,Benjamas 必須花費7 單位時間才能到達可逃出密室。
Sample #2:
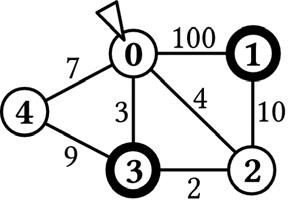
最佳的逃跑計畫如下:
•如果到了密室 0,就選擇通往密室3 的通道;如果這個通道被擋住了,就選擇通往密室2 的通道。
•如果到了密室 2,就選擇通往密室3 的通道;如果這個通道被擋住了,就選擇通往密室1 的通道。
•不用考慮密室 4,因為在這份逃跑計畫中根本不可能到達密室4。
在這計畫中, Benjamas 在14 單位時間內一定會到達有出口的密室。

密室用圓圈表示,連接密室的通道用直線表示。有出口的密室用粗圓圈表示。Benjamas 一開始在密室0(有三角形標示處)。一個最佳的逃跑計畫如下:
•如果到了密室 0,就選擇通往密室1 的通道;如果這個通道被擋住了,就選擇通往密室2 的通道。
•如果到了密室 2,就選擇通往密室3 的通道;如果這個通道被擋住了,就選擇通往密室4 的通道。
在最壞的情況下,Benjamas 必須花費7 單位時間才能到達可逃出密室。
Sample #2:

最佳的逃跑計畫如下:
•如果到了密室 0,就選擇通往密室3 的通道;如果這個通道被擋住了,就選擇通往密室2 的通道。
•如果到了密室 2,就選擇通往密室3 的通道;如果這個通道被擋住了,就選擇通往密室1 的通道。
•不用考慮密室 4,因為在這份逃跑計畫中根本不可能到達密室4。
在這計畫中, Benjamas 在14 單位時間內一定會到達有出口的密室。
Source:
IOI 2011Problem Setter
hanhan0912Testdata:
| Test | Time | Memory | Score |
|---|---|---|---|
| 0-1 | 2000ms | 262144kb | |
| 0-2 | 2000ms | 262144kb | |
| 1-1 | 2000ms | 262144kb | 46 |
| 1-2 | 2000ms | 262144kb | |
| 1-3 | 2000ms | 262144kb | |
| 1-4 | 2000ms | 262144kb | |
| 1-5 | 2000ms | 262144kb | |
| 1-6 | 2000ms | 262144kb | |
| 1-7 | 2000ms | 262144kb | |
| 1-8 | 2000ms | 262144kb | |
| 2-1 | 4000ms | 262144kb | 43 |
| 2-2 | 4000ms | 262144kb | |
| 2-3 | 4000ms | 262144kb | |
| 2-4 | 4000ms | 262144kb | |
| 2-5 | 4000ms | 262144kb | |
| 2-6 | 4000ms | 262144kb | |
| 2-7 | 4000ms | 262144kb | |
| 3-1 | 4000ms | 262144kb | 11 |
| 3-2 | 4000ms | 262144kb | |
| 3-3 | 4000ms | 262144kb | |
| 3-4 | 4000ms | 262144kb | |
| 3-5 | 4000ms | 262144kb | |
| 3-6 | 4000ms | 262144kb | |
| 3-7 | 4000ms | 262144kb |
NeoHOJ — The new era of HOJ
頁面讀取時間: 0.0268 秒,使用記憶體: 0.47MB 。
GitHub