修正 C++ 的程式碼在使用一定量動態記憶體後會產生 RF 的問題 @ 2019/12/6 4:45pm
Submit Ranklist
Problem : 273 - City
Problem Statistics
Solved Member: 15 Submission: 93 User Tried: 15Statement:
李奧納多像許多同年齡的義大利其他科學家和藝術家一樣,對城市規劃和城市設計非常感興趣。他的目標是建造一個理想的城市:要舒適、寬敞並能合理的使用資源,完成不像狹窄、幽閉的中世紀城市。
整個城市是由N個區塊組成,而這些區塊放在一個想像無限大的正方形網格上。每個格子可以使用一對坐標定位(列, 行)。格子(0,0)是網格中最左上方的格子。給定一個格子(i,j),它相鄰的格子是(如果它們存在的話):(i-1, j)、(i+1, j)、(i, j-1)和(i, j+1)。每一個區塊在網格上都剛好占滿一格。一個區塊可以放在格子(i , j)若且唯若滿足1 ≤ i, j ≤ 231 - 2 。我們使用網格的座標來定義放在上面的區塊。如果兩個區塊被放在相鄰的格子就視為相鄰。在一個理想的城市中,所有的區塊連接在一起,裡面沒有“洞”存在,也就是,區塊配置必須滿足以下兩個條件。
對於任何兩個“空”的格子,至少存在一連串相鄰的“空”格子連接它們。
對於任何兩個“非空”的格子,至少存在一連串相鄰的“非空”格子連接它們。
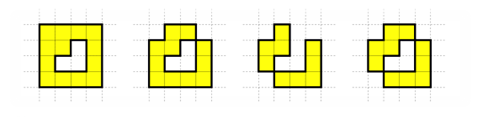
下面區塊的配置沒有一個算是理想的城市: 左邊兩個圖並不滿足第一個條件。第三個圖不滿足第二個條件,且第四個圖兩個條件都不滿足。
當在城市中移動時,一個跳躍的動作就表示從一個區塊移動到它相鄰的區塊。我們不能移動進入空的格子。假設v0, v1, …, vN 表示N個區塊的座標,對於任兩個不同的區塊vi 和vj ,他們的距離d(vi , vj)就是從區塊vi移動到區塊vj所需要的最少跳躍個數。
你的任務是要寫一個程式來計算一個理想城市中所有的區塊配對v 和v 的距離總和,且i < j。
也就是,你的程式必須計算以下總和:Σ d(vi , vj), where 0 ≤ i < j ≤ N-1
整個城市是由N個區塊組成,而這些區塊放在一個想像無限大的正方形網格上。每個格子可以使用一對坐標定位(列, 行)。格子(0,0)是網格中最左上方的格子。給定一個格子(i,j),它相鄰的格子是(如果它們存在的話):(i-1, j)、(i+1, j)、(i, j-1)和(i, j+1)。每一個區塊在網格上都剛好占滿一格。一個區塊可以放在格子(i , j)若且唯若滿足1 ≤ i, j ≤ 231 - 2 。我們使用網格的座標來定義放在上面的區塊。如果兩個區塊被放在相鄰的格子就視為相鄰。在一個理想的城市中,所有的區塊連接在一起,裡面沒有“洞”存在,也就是,區塊配置必須滿足以下兩個條件。
對於任何兩個“空”的格子,至少存在一連串相鄰的“空”格子連接它們。
對於任何兩個“非空”的格子,至少存在一連串相鄰的“非空”格子連接它們。
下面區塊的配置沒有一個算是理想的城市: 左邊兩個圖並不滿足第一個條件。第三個圖不滿足第二個條件,且第四個圖兩個條件都不滿足。

當在城市中移動時,一個跳躍的動作就表示從一個區塊移動到它相鄰的區塊。我們不能移動進入空的格子。假設v0, v1, …, vN 表示N個區塊的座標,對於任兩個不同的區塊vi 和vj ,他們的距離d(vi , vj)就是從區塊vi移動到區塊vj所需要的最少跳躍個數。
你的任務是要寫一個程式來計算一個理想城市中所有的區塊配對v 和v 的距離總和,且i < j。
也就是,你的程式必須計算以下總和:Σ d(vi , vj), where 0 ≤ i < j ≤ N-1
Input:Output:
第1行:N。
第2,...,N+1行:Xi Yi,其中0 ≤ i ≤ N-1, 1 ≤ Xi, Yi ≤ 231 - 2。
Subtask 1 (11 point)
N ≤ 200
Subtask 2 (21 point)
N ≤ 2000
Subtask 3 (23 point)
N ≤ 100 000
此外,下面兩個條件成立: 對於任兩個非空格子 i 和 j 且Xi = Xj時,所有在他們之間的格子也都是非空的。同時對於任兩個非空格子 i 和 j 且Yi = Yj時,所有在他們之間的格子也都是非空的。
Subtask 4 (45 point)
N ≤ 100 000
第2,...,N+1行:Xi Yi,其中0 ≤ i ≤ N-1, 1 ≤ Xi, Yi ≤ 231 - 2。
Subtask 1 (11 point)
N ≤ 200
Subtask 2 (21 point)
N ≤ 2000
Subtask 3 (23 point)
N ≤ 100 000
此外,下面兩個條件成立: 對於任兩個非空格子 i 和 j 且Xi = Xj時,所有在他們之間的格子也都是非空的。同時對於任兩個非空格子 i 和 j 且Yi = Yj時,所有在他們之間的格子也都是非空的。
Subtask 4 (45 point)
N ≤ 100 000
最後結果可能會超過32位元範圍,所以你必須將結果 module 1,000,000,000。
Sample Input:Sample Output:
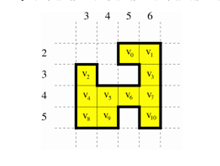
11
2 5
2 6
3 3
3 6
4 3
4 4
4 5
4 6
5 3
5 4
5 6
2 5
2 6
3 3
3 6
4 3
4 4
4 5
4 6
5 3
5 4
5 6
174
HINT:
範例測資的圖片

Source:
IOI 2012Problem Setter
hanhan0912Testdata:
| Test | Time | Memory | Score |
|---|---|---|---|
| 0 | 1000ms | 262144kb | |
| 1-1 | 1000ms | 262144kb | 11 |
| 1-2 | 1000ms | 262144kb | |
| 1-3 | 1000ms | 262144kb | |
| 1-4 | 1000ms | 262144kb | |
| 1-5 | 1000ms | 262144kb | |
| 1-6 | 1000ms | 262144kb | |
| 1-7 | 1000ms | 262144kb | |
| 1-8 | 1000ms | 262144kb | |
| 1-9 | 1000ms | 262144kb | |
| 1-10 | 1000ms | 262144kb | |
| 2-1 | 1000ms | 262144kb | 21 |
| 2-2 | 1000ms | 262144kb | |
| 2-3 | 1000ms | 262144kb | |
| 2-4 | 1000ms | 262144kb | |
| 2-5 | 1000ms | 262144kb | |
| 2-6 | 1000ms | 262144kb | |
| 2-7 | 1000ms | 262144kb | |
| 2-8 | 1000ms | 262144kb | |
| 2-9 | 1000ms | 262144kb | |
| 2-10 | 1000ms | 262144kb | |
| 3-1 | 1000ms | 262144kb | 23 |
| 3-2 | 1000ms | 262144kb | |
| 3-3 | 1000ms | 262144kb | |
| 3-4 | 1000ms | 262144kb | |
| 3-5 | 1000ms | 262144kb | |
| 3-6 | 1000ms | 262144kb | |
| 3-7 | 1000ms | 262144kb | |
| 3-8 | 1000ms | 262144kb | |
| 3-9 | 1000ms | 262144kb | |
| 3-10 | 1000ms | 262144kb | |
| 4-1 | 1000ms | 262144kb | 45 |
| 4-2 | 1000ms | 262144kb | |
| 4-3 | 1000ms | 262144kb | |
| 4-4 | 1000ms | 262144kb | |
| 4-5 | 1000ms | 262144kb | |
| 4-6 | 1000ms | 262144kb | |
| 4-7 | 1000ms | 262144kb | |
| 4-8 | 1000ms | 262144kb | |
| 4-9 | 1000ms | 262144kb | |
| 4-10 | 1000ms | 262144kb |
NeoHOJ — The new era of HOJ
頁面讀取時間: 0.0063 秒,使用記憶體: 0.47MB 。
GitHub