修正 C++ 的程式碼在使用一定量動態記憶體後會產生 RF 的問題 @ 2019/12/6 4:45pm
Submit Ranklist
Problem : 39 - 餐廳評鑑
Problem Statistics
Solved Member: 32 Submission: 95 User Tried: 35Statement:
台灣是吃的王國,到處都有好吃的餐廳。有鑑於此,身為雜誌編輯的小明,決定每週出一本餐廳週刊專門介紹各地值得推薦的好餐廳;每一本週刊由一名特派員負責到各個地區的餐廳親身體驗後,在週刊上對每間餐廳寫評語、給分數。每位特派員可以自己決定最高的級分,例如特派員Damon通常會用10級分代表滿分(如圖一),而特派員Chandler只用5級分代表滿分(如圖二)。而週刊銷售一段時間後,小明也會讓讀者回饋吃了之後的感想,讀者可以根據自身吃過的經驗,依照特派員的評分表來回饋評價。
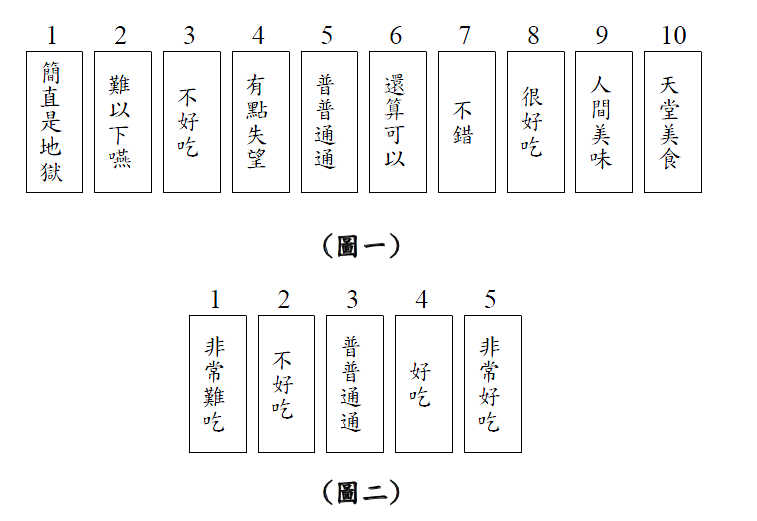
然而,可能在某位特派員眼中A餐廳只有到"還算可以"(6級分/10級分)的程度,但民眾吃過後通常都反應"很好吃"(8級分/10級分)。這種情形通常會發生在給分比較嚴格的特派員,反之也有給分比較寬鬆的特派員,但由於每本週刊都只有一位特派員負責,因此只要給分標準一致,基本上都沒有太大的問題。
不過,小明卻發現有些餐廳相較之下在週刊上的評價與大部分民眾的反應並不一致,例如A餐廳在週刊中的評價高於B餐廳,但讀者們卻普遍反應B餐廳比A餐廳好。為此,小明召開了會議,要每位特派員更用心的比較每家餐廳的優劣,才不會與民眾的反應落差太大造成讀者覺得週刊雜誌不夠專業。因此小明提出了一套計算評價差異的方式,若經過計算後週刊的評價與民眾的反應相去不遠,則會給負責該期週刊的特派員獎賞。假設在某期週刊中總共評價了k家餐廳,特派員對第i家餐廳的評分為si級分,透過讀者反應得到第i家餐廳的平均級分為ri,則計分方式如下(小明將此分數稱為"差異分數",差異分數越低表示特派員的評價與民眾反應越符合):
差異分數= $(i, j) | (s_i > s_j \text{ AND } r_i < r_j) \text{ OR } (s_i < s_j \text{ AND } r_i > r_j)$ , $1 \leq i < j \leq k$
舉例來說,假設某期週刊介紹了A、B、C、D、E五家餐廳,特派員分別給了3、7、5、5、8的分數,而統計了讀者回饋的分數平均後五家餐廳分別得到了4、6、7、5、8的分數,那麼差異分數計算後為1,其原因為B餐廳和C餐廳特派員與大部分的讀者感覺有落差(兩家餐廳相較之下,特派員給了B餐廳較高的分數,但讀者給了C餐廳較高的分數)。請注意C餐廳與D餐廳在特派員的評價中一樣好,但讀者回饋的分數C餐廳較高,這並不算一個落差。若讀者回饋的平均分數五家餐廳分別得到4、6、7、7、7,則差異分數為2,其原因為特派員以及讀者在B餐廳和C餐廳、以及B餐廳和D餐廳的評分有落差。由於每本週刊裡介紹的餐廳數目以及特派員的滿分標準都不同,因此小明請你寫一個程式來計算差異分數,好讓他分發獎賞給差異分數符合他標準的特派員。

然而,可能在某位特派員眼中A餐廳只有到"還算可以"(6級分/10級分)的程度,但民眾吃過後通常都反應"很好吃"(8級分/10級分)。這種情形通常會發生在給分比較嚴格的特派員,反之也有給分比較寬鬆的特派員,但由於每本週刊都只有一位特派員負責,因此只要給分標準一致,基本上都沒有太大的問題。
不過,小明卻發現有些餐廳相較之下在週刊上的評價與大部分民眾的反應並不一致,例如A餐廳在週刊中的評價高於B餐廳,但讀者們卻普遍反應B餐廳比A餐廳好。為此,小明召開了會議,要每位特派員更用心的比較每家餐廳的優劣,才不會與民眾的反應落差太大造成讀者覺得週刊雜誌不夠專業。因此小明提出了一套計算評價差異的方式,若經過計算後週刊的評價與民眾的反應相去不遠,則會給負責該期週刊的特派員獎賞。假設在某期週刊中總共評價了k家餐廳,特派員對第i家餐廳的評分為si級分,透過讀者反應得到第i家餐廳的平均級分為ri,則計分方式如下(小明將此分數稱為"差異分數",差異分數越低表示特派員的評價與民眾反應越符合):
差異分數= $(i, j) | (s_i > s_j \text{ AND } r_i < r_j) \text{ OR } (s_i < s_j \text{ AND } r_i > r_j)$ , $1 \leq i < j \leq k$
舉例來說,假設某期週刊介紹了A、B、C、D、E五家餐廳,特派員分別給了3、7、5、5、8的分數,而統計了讀者回饋的分數平均後五家餐廳分別得到了4、6、7、5、8的分數,那麼差異分數計算後為1,其原因為B餐廳和C餐廳特派員與大部分的讀者感覺有落差(兩家餐廳相較之下,特派員給了B餐廳較高的分數,但讀者給了C餐廳較高的分數)。請注意C餐廳與D餐廳在特派員的評價中一樣好,但讀者回饋的分數C餐廳較高,這並不算一個落差。若讀者回饋的平均分數五家餐廳分別得到4、6、7、7、7,則差異分數為2,其原因為特派員以及讀者在B餐廳和C餐廳、以及B餐廳和D餐廳的評分有落差。由於每本週刊裡介紹的餐廳數目以及特派員的滿分標準都不同,因此小明請你寫一個程式來計算差異分數,好讓他分發獎賞給差異分數符合他標準的特派員。
Input:Output:
測試資料共有三行。第一行有兩個正整數k和m (5 ≤ k ≤ 100000,m ≤ 2000000000,k與m由空白隔開),分別代表被評比的餐廳數目,以及特派員的滿級分。接下來的兩行各包含了k個介於1到m的整數(整數間由空白隔開),分別代表了特派員以及週刊讀者對每家餐廳所給的分數。
請根據小明提供的算式,計算出差異分數。
Sample Input:Sample Output:
SAMPLE 1:
5 10
3 7 5 5 8
4 6 7 5 8
SAMPLE 2:
5 10
3 7 5 5 8
4 6 7 7 7
5 10
3 7 5 5 8
4 6 7 5 8
SAMPLE 2:
5 10
3 7 5 5 8
4 6 7 7 7
SAMPLE 1:
1
SAMPLE 2:
2
1
SAMPLE 2:
2
Source:
TOI 2010Problem Setter
NekosyndromeTestdata:
| Test | Time | Memory | Score |
|---|---|---|---|
| 0-1 | 2000ms | 65536kb | |
| 0-2 | 2000ms | 65536kb | |
| 1 | 2000ms | 65536kb | 20 |
| 2 | 2000ms | 65536kb | 20 |
| 3 | 2000ms | 65536kb | 20 |
| 4 | 2000ms | 65536kb | 20 |
| 5 | 2000ms | 65536kb | 20 |
NeoHOJ — The new era of HOJ
頁面讀取時間: 0.0127 秒,使用記憶體: 0.45MB 。
GitHub