修正 C++ 的程式碼在使用一定量動態記憶體後會產生 RF 的問題 @ 2019/12/6 4:45pm
Submit Ranklist
Problem : 399 - 訓練計畫
Problem Statistics
Solved Member: 17 Submission: 71 User Tried: 19Statement:
ACM ICPC是一個給大學生組隊參加的程式競賽,參與競賽的也常常是高中就參加OI的選手。而某条更是其中的佼佼者,不僅在區域賽拿下了好成績,還代表了T大去參加總決賽。如今為了讓自己獲得更高的實力,打敗總決賽中的各個高手,某条決定展開一系列的練習。
某条在參考了他人訓練方式很久以後,決定訂出自己的訓練方案,列出了許多他要練習的項目,而每個練習項目分別有其所需要的練習時間。但故事並不是這麼單純,這些練習項目間可能是有關聯的,就如你要學習最短路徑算法前,你必須先學會如何存取一張圖。某条除了列出這些項目,也將項目間的關聯找了出來,即在練習某項目之前,某条必須先具備一些前置知識,曾經先練習過一些項目才行。當然,這些項目的依賴關係並不會有環狀出現,只要找到一個好順序,某条總是可以好好的全部練習完。
身為一個要參加總決賽的人,總是身懷某些特異功能,某条擁有可以平行訓練自己的能力。若當前有多個練習項目可以練習,他可以同時展開這些項目的練習,而且一次能練習的項目數並沒有任何上限!當然,前提是某條已經將這些項目的前置知識已經練習完了。當某条在平行練習一些項目時,若有個項目的前置知識也都練習完了,那某条可以不必等其他進行中的項目結束,直接開始練習這個項目。這令某条在練習上所需要的時間大大減少,也難怪某条可以打敗其他高手,獲得代表T大去參加ACM ICPC總決賽的權利。
聰明的你馬上發現,某条練習時間其實並不是所有練習項目加起來那麼簡單而已!如下圖:
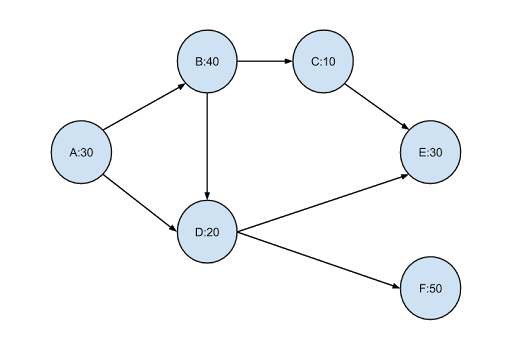
假定某条從時間點0開始訓練,那麼完成每個項目的時間點為:
● A: 30
● B: 70
● C: 80
● D: 90
● E: 120
● F: 140
如果你以為某条只是要你幫助他找出他最少要花多少時間才可以完成全部的練習項目,那你就太天真了。邪惡的某条其實是很邪惡的,雖然他很認真地整理出了屬於他的練習計畫,但他還是會想稍微偷懶的!但一次偷懶過多項目,很容易被發現,所以他決定只偷懶一個項目。為了在總決賽獲得好成績,某条覺得即使他偷懶,他也不該讓最後完成時間延後,因此某条想要詢問你,對於每個項目,如果他只打算在該項目偷懶,他最多可以偷懶多少單位的時間?
如上圖,他可以在項目C偷懶30單位時間,卻仍不影響完成全部項目的總時間。
某条在參考了他人訓練方式很久以後,決定訂出自己的訓練方案,列出了許多他要練習的項目,而每個練習項目分別有其所需要的練習時間。但故事並不是這麼單純,這些練習項目間可能是有關聯的,就如你要學習最短路徑算法前,你必須先學會如何存取一張圖。某条除了列出這些項目,也將項目間的關聯找了出來,即在練習某項目之前,某条必須先具備一些前置知識,曾經先練習過一些項目才行。當然,這些項目的依賴關係並不會有環狀出現,只要找到一個好順序,某条總是可以好好的全部練習完。
身為一個要參加總決賽的人,總是身懷某些特異功能,某条擁有可以平行訓練自己的能力。若當前有多個練習項目可以練習,他可以同時展開這些項目的練習,而且一次能練習的項目數並沒有任何上限!當然,前提是某條已經將這些項目的前置知識已經練習完了。當某条在平行練習一些項目時,若有個項目的前置知識也都練習完了,那某条可以不必等其他進行中的項目結束,直接開始練習這個項目。這令某条在練習上所需要的時間大大減少,也難怪某条可以打敗其他高手,獲得代表T大去參加ACM ICPC總決賽的權利。
聰明的你馬上發現,某条練習時間其實並不是所有練習項目加起來那麼簡單而已!如下圖:

假定某条從時間點0開始訓練,那麼完成每個項目的時間點為:
● A: 30
● B: 70
● C: 80
● D: 90
● E: 120
● F: 140
如果你以為某条只是要你幫助他找出他最少要花多少時間才可以完成全部的練習項目,那你就太天真了。邪惡的某条其實是很邪惡的,雖然他很認真地整理出了屬於他的練習計畫,但他還是會想稍微偷懶的!但一次偷懶過多項目,很容易被發現,所以他決定只偷懶一個項目。為了在總決賽獲得好成績,某条覺得即使他偷懶,他也不該讓最後完成時間延後,因此某条想要詢問你,對於每個項目,如果他只打算在該項目偷懶,他最多可以偷懶多少單位的時間?
如上圖,他可以在項目C偷懶30單位時間,卻仍不影響完成全部項目的總時間。
Input:Output:
第一行有兩個以空白隔開的整數N, M,表示某条所規劃的項目數與這些項目間的前置關係數。
第二行有N個正整數Ai,依序表示該項目所需花費的練習時間。
接下來有M行,每行有兩個整數ui, vi,表示第ui個項目是第vi個項目的前置知識之一。
Subtask 1:(20分)
1 ≤ N,Ai ≤ 1000
0 ≤ M ≤ 1000
1 ≤ ui < vi ≤ N
Subtask 2:(30分)
1 ≤ N ≤ 100000
M = N-1
1 ≤ Ai ≤ 100000
所有項目至多只會有一個前置項目
1 ≤ ui < vi ≤ N
Subtask 3:(50分)
1 ≤ N ≤ 100000
0 ≤ M ≤ 200000
1 ≤ Ai ≤ 100000
1 ≤ ui < vi ≤ N
第二行有N個正整數Ai,依序表示該項目所需花費的練習時間。
接下來有M行,每行有兩個整數ui, vi,表示第ui個項目是第vi個項目的前置知識之一。
Subtask 1:(20分)
1 ≤ N,Ai ≤ 1000
0 ≤ M ≤ 1000
1 ≤ ui < vi ≤ N
Subtask 2:(30分)
1 ≤ N ≤ 100000
M = N-1
1 ≤ Ai ≤ 100000
所有項目至多只會有一個前置項目
1 ≤ ui < vi ≤ N
Subtask 3:(50分)
1 ≤ N ≤ 100000
0 ≤ M ≤ 200000
1 ≤ Ai ≤ 100000
1 ≤ ui < vi ≤ N
輸出N個數字,第i行表示第i個項目所能偷懶的最大時間。
Sample Input:Sample Output:
6 7
30 40 10 20 30 50
1 2
1 4
2 3
2 4
3 5
4 5
4 6
30 40 10 20 30 50
1 2
1 4
2 3
2 4
3 5
4 5
4 6
0
0
30
0
20
0
0
30
0
20
0
Source:
104資奧校內初選Problem Setter
hanhan0912Testdata:
| Test | Time | Memory | Score |
|---|---|---|---|
| 0 | 500ms | 262144kb | |
| 1-1 | 500ms | 262144kb | 20 |
| 1-2 | 500ms | 262144kb | |
| 1-3 | 500ms | 262144kb | |
| 1-4 | 500ms | 262144kb | |
| 1-5 | 500ms | 262144kb | |
| 1-6 | 500ms | 262144kb | |
| 1-7 | 500ms | 262144kb | |
| 1-8 | 500ms | 262144kb | |
| 1-9 | 500ms | 262144kb | |
| 1-10 | 500ms | 262144kb | |
| 1-11 | 500ms | 262144kb | |
| 1-12 | 500ms | 262144kb | |
| 1-13 | 500ms | 262144kb | |
| 1-14 | 500ms | 262144kb | |
| 1-15 | 500ms | 262144kb | |
| 1-16 | 500ms | 262144kb | |
| 1-17 | 500ms | 262144kb | |
| 1-18 | 500ms | 262144kb | |
| 1-19 | 500ms | 262144kb | |
| 1-20 | 500ms | 262144kb | |
| 1-21 | 500ms | 262144kb | |
| 1-22 | 500ms | 262144kb | |
| 1-23 | 500ms | 262144kb | |
| 1-24 | 500ms | 262144kb | |
| 1-25 | 500ms | 262144kb | |
| 1-26 | 500ms | 262144kb | |
| 1-27 | 500ms | 262144kb | |
| 1-28 | 500ms | 262144kb | |
| 1-29 | 500ms | 262144kb | |
| 1-30 | 500ms | 262144kb | |
| 1-31 | 500ms | 262144kb | |
| 1-32 | 500ms | 262144kb | |
| 1-33 | 500ms | 262144kb | |
| 1-34 | 500ms | 262144kb | |
| 1-35 | 500ms | 262144kb | |
| 1-36 | 500ms | 262144kb | |
| 1-37 | 500ms | 262144kb | |
| 1-38 | 500ms | 262144kb | |
| 1-39 | 500ms | 262144kb | |
| 1-40 | 500ms | 262144kb | |
| 2-1 | 500ms | 262144kb | 30 |
| 2-2 | 500ms | 262144kb | |
| 2-3 | 500ms | 262144kb | |
| 2-4 | 500ms | 262144kb | |
| 2-5 | 500ms | 262144kb | |
| 2-6 | 500ms | 262144kb | |
| 2-7 | 500ms | 262144kb | |
| 2-8 | 500ms | 262144kb | |
| 2-9 | 500ms | 262144kb | |
| 2-10 | 500ms | 262144kb | |
| 2-11 | 500ms | 262144kb | |
| 2-12 | 500ms | 262144kb | |
| 2-13 | 500ms | 262144kb | |
| 2-14 | 500ms | 262144kb | |
| 2-15 | 500ms | 262144kb | |
| 2-16 | 500ms | 262144kb | |
| 2-17 | 500ms | 262144kb | |
| 2-18 | 500ms | 262144kb | |
| 2-19 | 500ms | 262144kb | |
| 2-20 | 500ms | 262144kb | |
| 2-21 | 500ms | 262144kb | |
| 2-22 | 500ms | 262144kb | |
| 2-23 | 500ms | 262144kb | |
| 2-24 | 500ms | 262144kb | |
| 2-25 | 500ms | 262144kb | |
| 3-1 | 500ms | 262144kb | 50 |
| 3-2 | 500ms | 262144kb | |
| 3-3 | 500ms | 262144kb | |
| 3-4 | 500ms | 262144kb | |
| 3-5 | 500ms | 262144kb | |
| 3-6 | 500ms | 262144kb | |
| 3-7 | 500ms | 262144kb | |
| 3-8 | 500ms | 262144kb | |
| 3-9 | 500ms | 262144kb | |
| 3-10 | 500ms | 262144kb | |
| 3-11 | 500ms | 262144kb | |
| 3-12 | 500ms | 262144kb | |
| 3-13 | 500ms | 262144kb | |
| 3-14 | 500ms | 262144kb | |
| 3-15 | 500ms | 262144kb | |
| 3-16 | 500ms | 262144kb | |
| 3-17 | 500ms | 262144kb | |
| 3-18 | 500ms | 262144kb | |
| 3-19 | 500ms | 262144kb | |
| 3-20 | 500ms | 262144kb | |
| 3-21 | 500ms | 262144kb | |
| 3-22 | 500ms | 262144kb | |
| 3-23 | 500ms | 262144kb | |
| 3-24 | 500ms | 262144kb | |
| 3-25 | 500ms | 262144kb | |
| 3-26 | 500ms | 262144kb | |
| 3-27 | 500ms | 262144kb | |
| 3-28 | 500ms | 262144kb | |
| 3-29 | 500ms | 262144kb | |
| 3-30 | 500ms | 262144kb | |
| 3-31 | 500ms | 262144kb | |
| 3-32 | 500ms | 262144kb | |
| 3-33 | 500ms | 262144kb | |
| 3-34 | 500ms | 262144kb | |
| 3-35 | 500ms | 262144kb |
NeoHOJ — The new era of HOJ
頁面讀取時間: 0.0093 秒,使用記憶體: 0.51MB 。
GitHub